알고리즘 복잡도

알고리즘 복잡도

알고리즘의 성능을 나타내는 척도

1) 시간 복잡도

어떤 문제를 해결하기 위한 알고리즘의 필요 연산 횟수(Step)

이러한 시간 복잡도를 줄이기 위해 데이터에 맞는 검색방법, 정렬방법, 자료구조 등이 필요해지는 것!!!

*물리적인 시간(분, 초 등)은 컴퓨터 하드웨어에 기인하기 때문에 알고리즘 복잡도에서 말하는 시간은 ‘연산횟수’임.

배열에서 어떤 값을 찾기 위해 Index 0 부터 순차적으로 검색해 나간다면(선형 검색), 그 알고리즘에서는 Index 0 부터 필요한 값을 찾는 순간까지가 연산 횟수(Step)이 됨.

• 빅-오: 최악의 경우

  *이 경우를 염두하고 프로그래밍을 해야겠지?

• 빅-오메가: 최적의 경우

• 빅-세타: 일반적인 경우

빅-오(Big-O) 표기

O(숫자)

입력값이 N개일 때, 괄호 안의 숫자만큼 연산이 진행됨을 표현함.

예시)

1) O(1) : N과 관계없이 연산횟수 1번.

2) O(log N) : 연산횟수가 log로 늘어남.

3) O(N) : 연산횟수가 N 선형으로 늘어남.

4) O(NlogN) : 연산횟수가 NlogN으로 늘어남. (=> Data크기가 100K정도까지는,,)

5) O(N^2) : 연산횟수가 N^2 지수함수로 늘어남. (=> Data크기가 1000정도까지는,,)

6) O(2^N) : 연산횟수가 2의 제곱으로 늘어남. (=> Data크기가 100정도까지는,,)

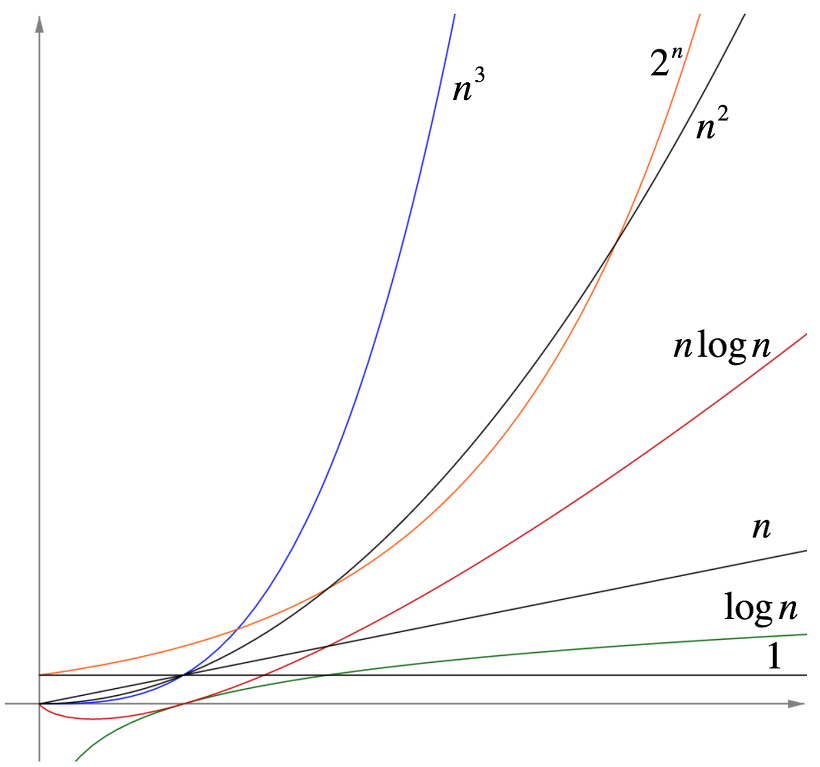
빅-오 표기는 ‘실제로 걸리는 Step’에 관심이 있다기 보다는,

입력값이 늘어날 때 Step이 어떤 방식*으로 증가하는지에 관심이 있다.

*상수에는 관심이 없다.

int[] arr = {1, 2, 3, 4, 5};

// O(1)
System.out.print(arr[0]);

// O(1) -> 상수에는 관심이 없다. 따라서 O(2)라고 표현하지 않는다.
System.out.print(arr[0]);
System.out.print(arr[0]);

// O(N)
for(int i = 0; i < arr.length(); i++) {
    System.out.print(arr[i]);
}

// O(N) -> 상수에는 관심이 없다. 따라서 O(2N)라고 표현하지 않는다.
for(int i = 0; i < arr.length(); i++) {
    System.out.print(arr[i]);
    System.out.print(arr[i]);
}

2) 공간 복잡도

어떤 문제를 해결하기 위한 알고리즘의 필요 메모리 량

요즘은 메모리용량이 과거보다 여유가 있기 때문에 차라리 메모리 사용량을 늘려 시간 복잡도를 줄이는 것에 더 초점이 맞추어져있음. (trade-off, 즉 무엇을 얻고 무엇을 잃을 것인가에 대한 문제)

---

마지막 수정일시: 2022-06-05 00:10